从一个浮点数运算说起

一个常见问题

1
2
3

$f1 = 0.58;
$f2 = 0.50;
echo (int)(($f1 - $f2) * 100);

结果为什么是 7 而不是 8，PHP出BUG了？我们换 Java 和 Go 试试。

1
2
3

float f1 = 0.58f;
float f2 = 0.50f;
System.out.println((int)((f1 - f2) * 100));

1
2
3

var f1 float32 = 0.58
var f2 float32 = 0.50
fmt.Println((int)((f1 - f2) * 100))

结果也都是7。
看来这是个“通病”。要弄清楚原因，我们得先回顾下以前学的基础知识。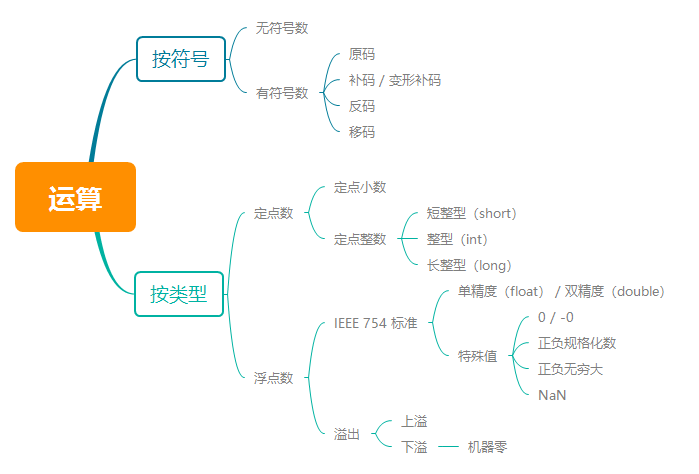

无符号数和有符号数

计算机中参与运算的数有两大类：无符号数和有符号数。
无符号数：没有符号位，寄存器中的每一位都用来存放数值，表示范围为 0 ~ 2ⁿ - 1。
有符号数：最高位为符号位，0表示正，1表示负，其余为数值位，表示范围为 -2^n-1 ~ +(2^n-1 - 1)（补码表示）。
eg. 机器字长（即，寄存器的位数）为 32 位，则无符号数表示范围为 0 ~ 2³² - 1，有符号数表示范围为 -2³¹ ~ +(2³¹ - 1)。

有符号数中，把符号“数字化”的数称为机器数，而把带“+”或“-”符号的数称为真值。

符号位如何参与运算？计算机规定了几种符号位和数值位的编码方式：原码、补码、反码、移码。

原码

符号位为0表示正数，符号位为1表示负数，eg. 1表示为0001，-1表示为1001。
为了区别整数和小数，约定整数的符号位与数值位之间用逗号隔开，小数的符号位与数值位之间用小数点隔开。
eg. +0.75（十进制）表示为0.11（二进制，0.11B = 2^-1 + 2^-2 = 0.5 + 0.25 = 0.75），-0.75表示为1.11；+3（十进制）表示为0,11，-3表示为1,11。
原码表示简单明了，但存在较多缺陷：

0的表示不唯一，即可以表示为0000（0），也可以表示为1000（-0）。
运算不便，比如 -4 + 3，得先用数值大的减去数值小的，最终结果的符号位以数值大的为准，这样导致加法运算却要用减法器实现。

补码

补码的意义在于，实现了用与负数等价的正数来替代，让加法器能实现减法操作。
还记得之前提到的时钟原理吗，可以回顾一下模和 同余数 的概念字符编码那点事。

修正下：其实之前讲的同余数就是补数（用补数更符合数学概念的定义），eg. +9 是 -3 以 12 为模的补数，记作 -3 ≡ 9（mod 12）。

eg. A = 9，B = 5，求 A - B（mod 12）。
A - B = 9 - 5 = 4（减法操作）
对于模 12 而言，-5 可以用其补数 +7 代替，所以，A - B = 9 + 7 = 16（作加法）。
而 12 会自动丢弃，所以，16 等价于 4，即， 4 ≡ 16（mod 12）。
进一步分析发现，时钟上的3点、15点都指向3的刻度，即，3 ≡ 15（mod 12） => 3 ≡ 3 + 12 ≡ 3（mod 12）。
这说明正数相对于“模”的补数就是正数自身，即，正数的补码等于原码。
同理，- 1011 ≡ + 0101（mod 2⁴），+ 0101 ≡ + 0101（mod 2⁴），- 0.1001 ≡ + 1.0111（mod 2¹），+ 0.1001 ≡ 0.1001（mod 2¹）。

小数中，当模数为 2² 时，形成了双符号位的补码，eg. -0.1001 对于 mod 2² 而言，补码为 11.0111。
这种双符号位的补码又称为变形补码，它在阶码运算和溢出判断中有其特殊作用。

反码

反码，主要用在负数中作为由原码求补码或由补码求原码的中间过渡。
正数的反码等于原码，负数的反码等于原码除符号位外按位取反。
负数求补码的简单方式即为：反码加1（加1是指末端数值位加1）；同时，原码与补码互为补数，所以由原码求补码或由补码求原码都可以用反码加1。

移码

虽然补码解决了减法操作，但很难用补码在直观上比较大小，eg. -3 的补码是 1,1101，+4 的补码是 0,0100，直观上看，会以为 1,1101 > 0,0100。
如果加上2ⁿ，情况就发生了变化，eg. - 0011（-3 的二进制） + 10000 = 01111 + 00001 - 0011 = 01101，0100（4 的二进制） + 10000 = 10100，10100 > 01101。
移码就是真值加2ⁿ（n为整数的位数），在数轴上相当于正向移动了2ⁿ个单元。
从结果可以看出，移码相当于符号位取反的补码，所以，移码的表示范围也为 -2^n-1 ~ +(2^n-1 - 1)。

最小真值的移码为0（eg. 16位二进制，补码对应的最小真值为-128，即 10000000，对应移码为 00000000），利用这一特点，浮点数的阶码用移码表示时，就能很方便地判断阶码的大小。

为了进一步理解，下面给出8位二进制在不同表示（无符号数、原码、补码、反码、移码）时所对应的真值：

二进制代码	无符号数对应的真值	原码对应的真值	补码对应的真值	反码对应的真值	移码对应的真值
`00000000`	0	+0	+0/-0	+0	-128
`00000001`	1	+1	+1	+1	-127
`00000010`	2	+2	+2	+2	-126
…	…	…	…	…	…
`01111110`	126	+126	+126	+126	-2
`01111111`	127	+127	+127	+127	-1
`10000000`	128	-0	-128	-127	+0/-0
`10000001`	129	-1	-127	-126	+1
`10000010`	130	-2	-126	-125	+2
…	…	…	…	…	…
`11111101`	253	-125	-3	-2	+125
`11111110`	254	-126	-2	-1	+126
`11111111`	255	-127	-1	-0	+127

计算机中，根据小数点位置是否固定，划分为浮点数和定点数。

定点数

小数点不再表示出来，而是约定在默认的固定位置。有两种格式：

小数点位于符号位和数值位之间，此时的机器数称为定点小数。
小数点位于数值位之后，此时的机器数称为定点整数。

表示范围分别为：

	定点整数	定点小数
原码	`-(2ⁿ - 1) ~ +(2ⁿ - 1)`	`-(1 - 2^-n) ~ +(1 - 2^-n)`
补码	`-2^n-1 ~ +(2^n-1 - 1)`	`-1 ~ +(1 - 2^-n)`
反码	`-(2ⁿ - 1) ~ +(2ⁿ - 1)`	`-(1 - 2^-n) ~ +(1 - 2^-n)`

浮点数

相对于定点数而言，浮点数利用指数使小数点的位置可以根据需要而上下浮动，从而可以灵活地表达更大范围的实数。
eg. 352.47 = 3.5247 × 10² = 3524.7 × 10^-1 = 0.3527 × 10³
用 N = S × r^j 表示浮点数，S 为尾数，j 为阶码，r 是基数。
以基数 r = 2 为例，11.0101 = 0.110101 × 2¹⁰ = 1.10101 × 2¹ = 1101.01 × 2^-10 = 0.00110101 × 2¹⁰⁰ = …
为了提高数据精度以及便于浮点数的比较，规定计算机中浮点数的尾数用纯小数形式，故 0.110101 × 2¹⁰ 和 0.00110101 × 2¹⁰⁰ 是可以采用的。
原码表示时，将尾数最高位为1的浮点数称为规格化数，即 N = 0.110101 × 2¹⁰ 为浮点数的规格化形式，此时精度最高。

表示格式

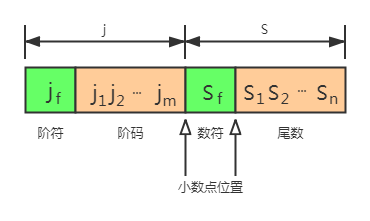
浮点数由阶码 j 和尾数 S 两部分组成。
阶码是整数形式，其位数m反映了浮点数的范围；尾数是小数形式，其位数n反映了浮点数的精度。
规格化浮点数的表示范围（原码表示）为：正数 2^{-(2^m - 1)} × 2^-1 ~ 2^{(2^m - 1)} × (1 - 2^-n)，负数 -2^{(2^m - 1)} × (1 - 2^-n) ~ -2^{-(2^m - 1)} × 2^-1。
通常，短实数（32位）阶码取8位（含阶符），尾数取24位（含数符）；长实数（64位），阶码取11位（含阶符），尾数取53位（含数符）。

上溢 & 下溢

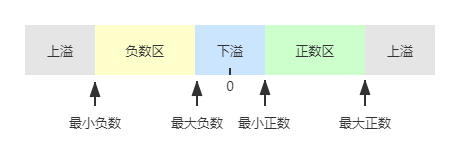
当阶码大于最大阶码时，称为上溢；此情况，程序报异常，需进行中断溢出处理。
当阶码小于最小阶码时，称为下溢；此情况，通常将尾数各位强置为0，按机器零处理，程序继续运行。

IEEE754标准

现今，浮点数一般采用 IEEE 754 标准：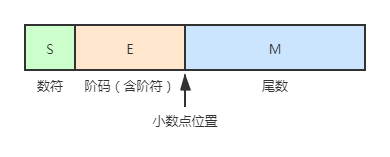

常用的浮点数有三种：

	符号位 S	阶码	尾数	总位数
短实数	1	8	23	32
长实数	1	11	52	64
临时实数	1	15	64	80

其中，阶码用移码表示，为阶码的真值加上一个偏移量（短实数时加 127，长实数时加 1023）；
尾数用补码表示，规格化表示，非“0”时最高位为 1，对短实数和长实数，此高位 1 隐藏。
举个栗子，十进制数 178.125，对应二进制数 10110010.001，二进制浮点表示 1.0110010001 × 2¹¹¹，短实数表示 0,10000110;01100100010000000000000。

真值公式

短实数，即，单精度浮点数，x = (-1)^S × (1.M) × 2^E - 127，e = E - 127
长实数，即，双精度浮点数，x = (-1)^S × (1.M) × 2^E - 1023，e = E - 1023

特殊值定义

IEEE754中规定了几个特殊值：

阶码全为0，尾数也全为0，表示的是0；根据不同的阶符（0正1负），可表示 +0 和 -0。
阶码全为0，尾数不全为0，表示正负规格化数；此时的阶码为-126，可以理解为把 1.M × 2^0 - 127转换成0.1M × 2^{0 - 127 + 1}。
阶码全为1，尾数全为0，根据阶符不同，表示正负无穷大。
阶码全为1，尾数不全为0，表示 NaN（Not a Number），即，不是一个数。

加减运算

现今，计算机中基本都采用补码作加减法运算。

定点数

基本公式

整数，[A]_补 + [B]_补 = [A + B]_补(mod 2^{n + 1})，[A - B]_补 = [A]_补 + [-B]_补(mod 2^{n + 1})
小数，[A]_补 + [B]_补 = [A + B]_补(mod 2)，[A - B]_补 = [A]_补 + [-B]_补(mod 2)
eg. A = 0.1011，B = 0.0101，求[A - B]_补。
解：[A - B]_补 = [A]_补 + [-B]_补 = 0.1011 + 1.1011 = 10.0110，按模2取值，丢弃最左边的1，结果为 0.0110。
eg. 8位机器字长（含符号位），A = +15，B = +24，求 [A - B]_补并还原成真值。
解：[A - B]_补 = [A]_补 + [-B]_补 = 0,0001111 + 1,1101000 = 1,1110111，A - B = -0001001 = -9。

溢出判断

运算结果超出了机器字长所能表示的范围，这种现象，称之为溢出。
比如，8位机器字长，A = -93，B = +45，则计算出来的[A - B]_补 = 10,1110110，按模2ⁿ⁺¹取值，丢弃最左边的1，结果为 0,1110110，A - B = +1110110 = +118，结果出错了。
为什么？这是因为 A - B = -138，而8位机器字长的有符号数能表示的真值范围为 -128 ~ +127，结果溢出了。
判断溢出有两种方法：

用1位符号位判断溢出：参与操作的两个数符号相同，但结果却与操作数的符号不同。
减法是用加法器实现的，上例中相当于两个负数相加，而结果却为正数，故，可以判断是溢出。

用2位符号位判断溢出：用变形补码作加法，当2位符号位不同时，表示溢出，否则，无溢出；高位符号位为结果的符号。

eg. x = +(11/16)，y = +(3/16)，用变形补码计算 x + y。
解：x = 0.1011，y = 0.0011
=> [x]变补 = 00.1011，[y]变补 = 00.0011
=> [x]变补 + [y]变补 = 00.1110
=> [x + y]变补 = 00,1110
符号位相同，无溢出，故 x + y = 0,1110

eg. x = +(11/16)，y = +(7/16)，用变形补码计算 x + y。
解：x = 0.1011，y = 0.0111
=> [x]变补 = 00.1011，[y]变补 = 00.0111
=> [x]变补 + [y]变补 = 01.0010
符号位不同，表示溢出。

注：用2位符号位判断溢出对整数也适用。

浮点数

浮点数加减运算的步骤：

对阶 - 使两数的小数点位置对齐。
小阶向大阶看齐原则：阶小的尾数向右移位，每右移一位，阶码加1，直至两数的阶码相等。
例如，x = 0.1101 × 2⁰¹，y = (-0.1010) × 2¹¹，求 x + y 时必须先对阶。
阶码相差 = [x 阶码]补 = [y 阶码]补 = [x 阶码]补 + [-y 阶码]补 = +01 + (-11) = 0,01 + 1,01 = 1,10 = -2。
将 x 的尾数右移两位，其阶码加2，得 x = 0.001101 × 2¹¹，假设尾数只有4位，需丢弃超出的数值位，得 x = 0.0011 × 2¹¹。
故，尾数右移可能会造成数值位丢失，影响精度。
尾数求和 - 将对阶后的两尾数按定点加减运算规则求和（差）。
上例中，两数对阶后，[x 尾数]变补 = 00.0011，[y 尾数]变补 = 11.0110，相加等于 11.1001。
注：用变形补码进行计算是为了便于后续的溢出判断。
规格化 - 为增加有效数字的位数，提高运算精度，将求和（差）后的尾数规格化。
分左规和右规。
- 左规 - 形如 00.0xxx 或 11.1xxx 时，尾数左移一位，阶码减1，直至符合规格化表示。
  上例中，[x 尾数 + y 尾数]变补 = 11.1001，需左规，得 11.0010，故 x + y = -0.1110 × 2¹⁰。
- 右规 - 形如 01.xxx 或 10.xxx 时，表示尾数溢出，需通过尾数右移一位，阶码加1进行处理。
舍入 - 为提高精度，需考虑尾数右移时丢失的数值位。
在对阶和右规时，常用如下两种舍入方法来提高尾数的精度：
- 0舍1入
  “0舍1入”类似于十进制数运算中的“四舍五入”，即，被移去的最高数值位（注：指移去的数值位中的最高位）为1，则在尾数的末位加1；否则，舍去。
  但，这种做法可能使尾数又溢出，此时需再做一次右规。
- 恒置1
  不论丢弃的最高数值位是1或0，都使右移后的尾数末位恒置1。
溢出判断 - 判断结果是否溢出。
尾数溢出并不表示结果溢出，只有右规后，再根据阶码来判断结果是否溢出，eg. 单精度浮点数的阶码的表示范围为 -128 ~ +127（补码表示）。
- 上溢 - 阶码的值超过了阶码所能表示的最大正数。
  若浮点数为正数，则为正上溢，记为 +∞，若浮点数为负数，则为负上溢，记为 -∞。
- 下溢 - 阶码的值超过了阶码所能表示的最小负数。
  下溢时，浮点数值趋于零，作为机器零看待。

举个栗子，设 x = 2^-101 × (-0.101000)，y = 2^-100 × (+0.111011)，阶符2位，阶码的数值部分3位，数符2位，尾数的数值部分6位，求 x - y。
解：[x]补 = 11,011;11.011000，[y]补 = 11,100;00.111011

对阶：小阶向大阶看齐，两数的阶码相差 = [x 阶码]补 - [y 阶码]补 = [x 阶码]补 + [-y 阶码]补 = -101 + 100 = 11,011 + 00,100 = 11,111，即，阶码相差 = -1，则x的尾数向右移1位，阶码+1，得 [x]补 = 11,100;11.101100。
尾数求和：[x 尾数]补 - [y 尾数]补 = [x 尾数]补 + [-y 尾数]补 = 11.101100 + 11.000101 = 10.110001，即，[x - y]补 = 11,100;10.110001。
规格化：尾数符号位为“10”，需右规，舍弃尾数最后一位数值位，得 [x - y]补 = 11,101;11.011000。
舍入：采用“0舍1入”，尾数右规时舍弃的末位数值位是1，故尾数加1，得 [x - y]补 = 11,101;11.011001。
溢出判断：[x - y]补的阶码为11,101，即 -011，没有溢出，故最终结果为 x - y = 2^-011 × (-0.100111)。

最初的问题

首先，我们可以发现，0.58 是无法精准转换为二进制的，即，0.58 = 0.100101000111101… = 1.00101000111101... × 2^-001。
而 PHP 和 Java 等都遵循 IEEE 754 浮点数表示规范，所以，双精度存储的尾数为 0010100011110101110000101000111101011100001010001111，转十进制得 0.57999999999999996。
因此，看似有穷的小数，在计算机的二进制表示里却是无穷的。
所以，0.58 - 0.50，实际上得到的是 0.07999…，再乘以 100 得 57.99999…（涉及浮点数乘法）。
而 PHP 中用 int 强制把浮点型转换为整型（效果同 intval 一样）时会直接舍弃非整型部分的数值，所以程序结果为 57。

几个问题

为什么补码可以表示的最小真值是 `-2^n-1`？

拿8位二进制来说，补码能表示的最小真值为 -2⁷ = -128，对应二进制为 1000 0000。
为了理解，我们先看来 -127，原码为 1111 1111，补码为 1000 0001。
可以看出，-127 的补码表示还可以再减1，即 1000 0001 - 1 = 1000 0000 = -128。
注：通常的进制转换主要用于无符号数，对于符号数的反码、补码、移码等表示，并不能直接用进制转换得出对应真值，需通过原码来转换。

为什么要用移码来表示阶码？

原因是便于浮点数加减运算时的对阶操作（即，比较大小）。
eg. 1.01 × 2^-1 + 1.11 × 2³
如果用补码来表示阶码，则-1的补码在机器中是111，3的补码是011，在机器中直接比较是111 > 011，不符。
而用移码可以解决这个问题，-1的移码表示为011（3），而3的移码表示为111（7），符合实际。

如何理解原码表示的规格化浮点数范围？

首先，原码表示的规格化浮点数的尾数最高位为1，所以n位尾数的原码表示范围为：正数 2^-1 ~ (1 - 2^-n)，负数 -(1 - 2^-n) ~ -2^-1。
同样，m位阶码的原码表示范围为：-(2^m - 1) ~ (2^m - 1)。

理解浮点数的规格化表示

规格化表示：原码表示时，尾数的最高数值位为1；补码表示时，尾数的最高数值位与符号位相异。
如何理解补码表示时的规格化定义？原码表示时，规格化数为 0.1xxx：
+ 0.1xxx 的补码为 0.1xxx，- 0.1xxx 的补码为 1.0xxx + 2^-n，若xxx不全为1，则结果为 1.0yyy，符合定义，但若xxx全为1，则结果为 1.1000，不符合定义。
所以，为了硬件判断，特规定 -(1/2) 不是规格化数。

浮点数可以精准表示 0 吗，如何理解机器零？

机器零指尾数全为 0 或阶码等于或小于最小阶码（eg. 若阶码用原码表示，则等于或小于 -(2^m - 1)）时，计算机都把浮点数当作零看待。
如果阶码用移码表示，尾数用补码表示，则，最小真值的阶码全为0 且真值为0的尾数也全为0，这样的机器零有利于简化机器中的判“0”电路。
另，IEEE 754 只对非“0”的有效位隐藏最高位 1，即，全 0 的情况下没有隐藏位，符合机器零，所以，浮点数可以精准表示 0。

定点数和浮点数的表示示例

16位浮点数，其中，阶码5位（含阶符），尾数11位（含数符）。

十进制数	二进制形式	定点数表示	定点数机器存储	浮点数规格化表示	浮点数机器存储
`+(13/128)`	`0.0001101000`	`0.0001101000`	原码=补码=反码=`0.0001101000`	`0.1101000000 × 2^-11`	原码 `1,0011;0.1101000000` 补码 `1,1101;0.1101000000` 反码 `1,1100;0.1101000000`
`-54`	`-110110`	`-0000110110`	原码 `1,0000110110` 补码 `1,1111001010` 反码 `1,1111001001`	`-(0.1101100000) × 2¹¹⁰`	原码 `0,0110;1.1101100000` 补码 `0,0110;1.0010100000` 反码 `0,0110;1.0010011111`
`-(53/512)`	`-0.0001101010`	`-0.0001101010`	原码 `1.0001101010` 补码 `1.1110010110` 反码 `1.1110010101`	`-(0.1101010000) × 2^-11`	原码 `1,0011;1.1101010000` 补码 `1,1101;1.0010110000` 反码 `1,1101;1.0010101111`

如果阶码用移码表示，尾数用补码表示，则 -(53/512) = 0,1101;1.0010110000。

为什么 IEEE754 中，32位浮点数的阶码偏移量是 127 而不是 128？

8位阶码的真值是 -127（- 111 1111） ~ +127（+ 111 1111），通常，移码为真值 + 2⁷，相当于符号位取反的补码。
但，IEEE754中保留了阶码全为1和全为0的情况（用于特殊值定义），这样，阶码表达的范围变成了 1 ~ 254，对应真值范围为 -126 ~ +127。
那么从 [1, 254] 对应到实际的真值范围 [-126, +127]，减去127就好了，这样就可以获得指数的真值了。
这个减去的 127 就是偏移量。

IEEE754浮点数表示示例

求 1.640625 × 2²⁰ 的单精度存储格式
1.640625 × 2²⁰ = 1.101001 × 2¹⁰¹⁰⁰ = 0,10010011;10100100000000000000000 = 49D20000H
求 B5D20000H 的真值
B5D20000H = 1,01101011;10100100000000000000000 = -1.101001 × 2^-10100 = -1.640625 × 2^-20
求 80510000H 的真值
80510000H = 1,00000000;10100010000000000000000 = -0.1010001 × 2^-126 = -0.640625 × 2^-126

既然 0.58 是无法精确存储的，为什么程序能精确输出 0.58？

$f1 = 0.58;
$f2 = 0.580000000000002;
$f3 = 0.579999999999996;
var_dump($f1);// float(0.58)
var_dump($f2);// float(0.58)
var_dump($f3);// float(0.58)

实际上，0.58、0.580000000000002 和 0.579999999999996 的存储形式是一样的，程序都当作是 0.58。怎么说？
若把浮点数能表示的所有数都画在一条数轴上，那么会看到能表示的两个数字之间是有间隔的，且在0附近的数值间隔要比其他地方小，即，0附近的数比较密集。
能表示的两个数字之间的数，在计算机看来都是同一个数。如 0.58、0.580000000000002、0.579999999999996 是同一个数。
这几个数按 IEEE 754 标准存到计算机中时，尾数23位满了，但后边还有，把后边的省略了；省略之后，剩下的全部一样，所以计算机认为它们是一个数。

常见面试题

为什么不要用 float / double 存储金额？

有丢失精度的风险，特别是在浮点运算时。
可以考虑以最小单位的整型方式存储，若确实需要用浮点数进行运算，可以考虑用语言提供的类库来处理。
eg. PHP可以用 BC Math 系列函数，Java可以用 BigDemical 类（通过字符串精准存储每一位数）。

参考资料

计算机组成原理（第2版）第6章计算机的运算方法
关于PHP浮点数你应该知道的，https://www.laruence.com/2011/12/19/2399.html
PHP浮点数的一个常见问题的解答，https://www.laruence.com/2013/03/26/2884.html
Float 浮点型，https://www.php.net/manual/zh/language.types.float.php
为什么要用移码来表示阶码，https://www.cnblogs.com/roscangjie/p/12237725.html
32位IEEE754的阶码偏移量为何用127而不是128，https://www.zhihu.com/question/24784136
浮点数0.7在Java中是无法精确存储的，却为何能精确输出0.7